استفاده از زوایا در تحلیل تکنیکال برای معاملهگران | رویکردی ساده و کاربردی
عملیات مبتنی بر زاویه از دیرباز در معاملات استفاده میشود. مزیت اصلی این نوع عملیات، سادگی در ساخت زوایا و وضوح در تفسیر آنهاست. ابزارهای گن نمونهای برجسته از این نوع عملیات هستند.
شاید تصور شود که همه چیز درباره زوایا پیشتر گفته شده است؛ اما قصد دارم از زاویهای متفاوت به این موضوع نگاه کنم. بیایید سعی کنیم مفاهیم قدیمی و فراموششده را بازبینی کنیم تا به ایدههای کاملاً جدیدی دست پیدا کنیم.
ساخت اولین زاویه
زاویه یکی از سادهترین اشکال هندسی است. کشیدن دو خط از یک نقطه چه چیزی سادهتر از این میتواند باشد؟ در اغلب موارد، یکی از این خطوط نمایانگر محور افقی (محور x) است.
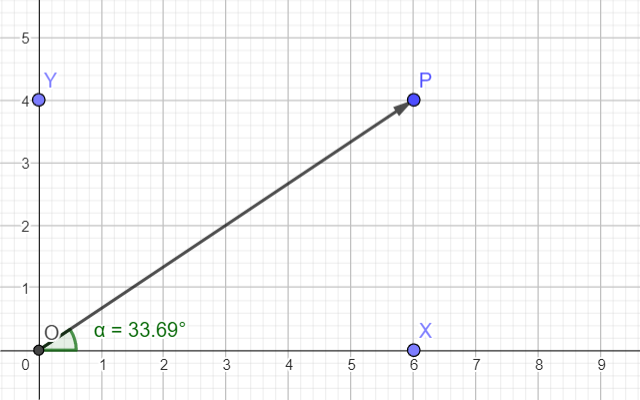
از آنجایی که زاویه یک مقدار بدون بُعد است، هر دو محور باید مقادیر یکسانی داشته باشند. اگر روی یک محور متر و روی محور دیگر کیلوگرم اندازهگیری کنید، تنها نوعی رابطه بین آنها بهدست خواهید آورد، نه یک زاویه.
حال بیایید عملیات زاویهمحور را به عنوان یک اندیکاتور پیادهسازی کنیم. در این اندیکاتور، جفت ارزهای مختلف روی محور X و Y نمایش داده میشوند. در این صورت، یک زاویه کوچک نشاندهنده قیمت بالا برای جفت ارز اول و قیمت پایین برای جفت ارز دوم است. به همین ترتیب، زاویه بزرگ نشان میدهد که قیمت نماد دوم بیشتر از نماد اول است. به عبارت دیگر، اندیکاتور ما حالت اشباع خرید یا فروش بیش از حد یک جفت ارز نسبت به جفت دیگر را نشان میدهد. ایده خوبی برای معاملات جفتی به نظر میرسد.
اولین چالشی که با آن مواجه میشویم این است که مقادیر محورهای مختلف متفاوت هستند (برای مثال، من EURUSD و USDJPY را انتخاب کردم). به سادگی میتوانیم این مشکل را با تقسیم قیمت هر ابزار بر مقدار پوینت آن حل کنیم.
با این کار، دو مشکل حل میشود – روی هر دو محور مقادیر قابل مقایسهای خواهیم داشت (قیمت به صورت پوینت)، و مقیاس روی این محورها یکسان خواهد بود. این همان چیزی است که اندیکاتور ما شبیه آن است.
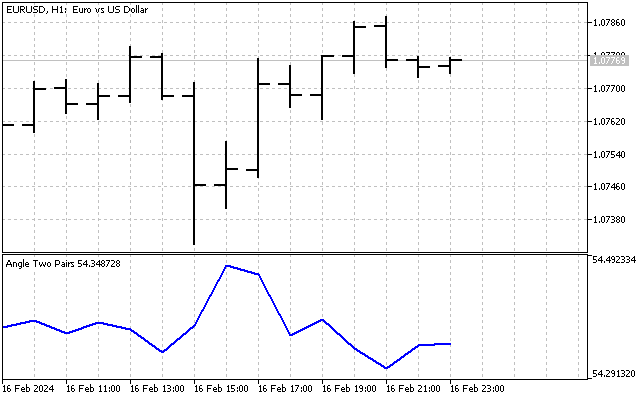
در نگاه اول، این اندیکاتور ساده بهنظر میرسد. مقدار آن حول یک مقدار میانگین نوسان میکند و اختلاف بین حداکثر و حداقل مقدار آن تنها ۲ تا ۳ درجه است. اما بیایید عجولانه قضاوت نکنیم؛ شاید بتوانیم این اندیکاتور را بهبود دهیم و آن را اطلاعاتیتر کنیم.
یادآوری کوچکی داشته باشیم. رایجترین واحد اندازهگیری زاویه که در زندگی روزمره استفاده میکنیم درجه است. برای محاسبات ریاضی، اغلب از رادیان استفاده میشود. تبدیل درجه به رادیان و بالعکس طبق معادلات زیر انجام میگیرد:
![]()
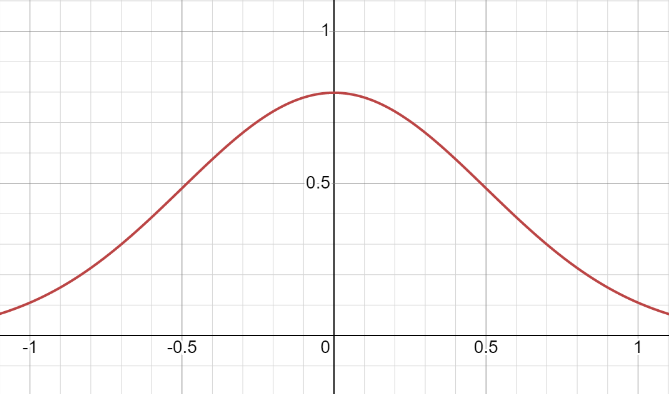
همانطور که میبینیم، توزیع پیچیده از میانگین و انحراف معیار استفاده میکند، درست مانند توزیع نرمال معمولی. جمعبندی در اینجا شاید کمی پیچیده به نظر برسد، اما هنگام کار با دادههای واقعی، بهراحتی از پس این بینهایتها برخواهیم آمد.
حال بیایید از شاخص خود استفاده کرده و توزیع نرمال پیچیده را روی آن اعمال کنیم.
ابتدا باید میانگین تمام زوایای موجود در تاریخچه را تعیین کنیم. در اینجا یافتن میانگین کار دشواری نیست – کافی است از جمع معمولی و تقسیم بر تعداد مشاهدات استفاده کنیم. اما در کل، میانگین زاویهای را باید بهطور متفاوتی به دست آورد. تصور کنید که میانگین دو زاویه – ۱۰ درجه و ۳۵۰ درجه – را باید پیدا کنیم. رویکرد معمول پاسخ ۱۸۰ درجه را میدهد، که پاسخ اشتباهی است. میانگین آنها صفر است.
برای به دست آوردن پاسخ صحیح در هر شرایطی، باید مراحل زیر را انجام دهیم: ابتدا جمع سینوسها و کسینوسهای تمام زوایا را محاسبه کنیم. سپس جمع اول را بر جمع دوم تقسیم کنیم تا تانژانت زاویه میانی را به دست آوریم.
![]()
اکنون، پیدا کردن مقدار میانگین زاویه کار دشواری نخواهد بود. اما در اینجا یک شرط کوچک نیز وجود دارد. اگر تمام زوایا بین -۹۰° و +۹۰° قرار داشته باشند، میتوانیم از تابع MathArctan استفاده کنیم. اما اگر زوایا فراتر از این محدودهها بروند، حتماً باید از تابع عمومیتری به نام MathArctan2 استفاده کنیم.
بنابراین، میانگین زاویه به صورت زیر محاسبه خواهد شد:
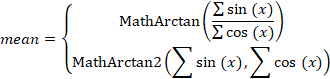
پس از اینکه مقدار میانگین زاویه را تخمین زدیم، میتوانیم به تخمین انحراف معیار بپردازیم. برای این کار میتوانیم از روش یامارتینو استفاده کنیم. ابتدا باید مقدار کمکی را پیدا کنیم:
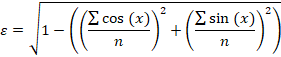
این روش تخمین نسبتاً دقیقی از انحراف معیار ارائه میدهد، اما میتوان آن را بهبود بخشید:
![]()
حال بیایید تغییراتی در اندیکاتور خود ایجاد کنیم. ابتدا، تفاوت بین زاویه فعلی و زاویه میانگین را محاسبه خواهیم کرد و سپس این تفاوت را با انحراف معیار مقایسه خواهیم کرد. در نهایت، نتیجه به شکل زیر خواهد بود.
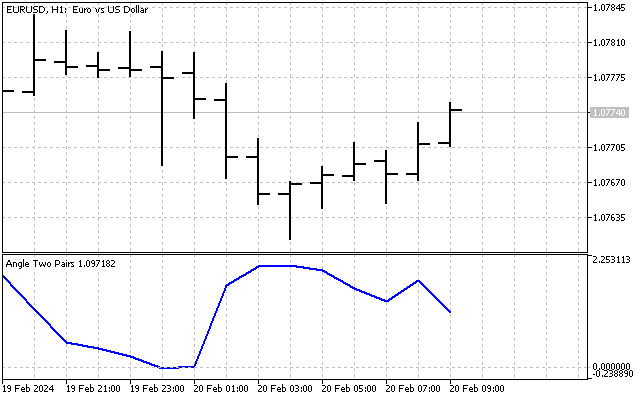
این اندیکاتور به ما این امکان را میدهد که سطوح خرید بیش از حد/فروش بیش از حد را با دقت بیشتری تعیین کنیم و نزدیکترین معادل آن اندیکاتور CCI است.
زوایا و تابع خطی
ما با زوایا در دادههای مشابه کار کردهایم. آیا میتوان عملیاتهای زاویهای را به یک روند اعمال کرد؟ پاسخ منفی است، زیرا با انواع مختلف دادهها سر و کار داریم؛ یکی از محورها زمان و دیگری قیمت است.
خب، پاسخ صحیح است، اما در عین حال نادرست نیز هست. بیایید تابع خطی را به خاطر بیاوریم. تابع خطی یک رابطه خطی بین دو متغیر مستقل را توصیف میکند و به وسیلهی معادله زیر بیان میشود:
![]()
زاویه در اینجا کجاست؟ این زاویه در نسبت \(k\) نهفته است. این نسبت برابر با تانژانت زاویه شیب خط نسبت به محور \(X\) است.
بیایید سعی کنیم از این تابع برای توصیف یک روند استفاده کنیم. معادله تابع خطی برای معاملهگران به شکل زیر خواهد بود:
![]()
در این حالت، نسبت \(k\) تفسیر دیگری پیدا میکند؛ این نسبت نشاندهنده تغییر متوسط قیمت به ازای هر واحد زمان است. یک نکته کوچک دیگر: من زمان را به معادله وارد کردم، اما در محاسبات واقعی، استفاده از شاخصها به جای زمان بسیار سادهتر است. اولاً، تعطیلات و آخر هفتهها تأثیر زیادی بر دقت محاسبات دارند. و ثانیاً، استفاده از شاخصها معادلات (و محاسبات) را بسیار سادهتر میکند. تنها الزامی که برای این شاخصها وجود دارد این است که باید از چپ به راست افزایش یابند.
حال بیایید نگاهی به روشهای برآورد پارامترهای روند خطی بیندازیم. اول از همه، میتوانیم از روش حداقل مربعات (LSM) استفاده کنیم. اجازه دهید یادآوری کنم که به جای زمان، از شاخصهایی استفاده میکنم که مقادیر آنها از ۰ تا \(n-1\) تغییر میکند.
![]()
![]()
اما روشهای قابل اعتمادتر دیگری نیز برای ارزیابی این پارامترها وجود دارد. به عنوان مثال، میتوانیم از تخمین تیل-سن (Theil-Sen estimate) استفاده کنیم. بیایید ببینیم این ارزیابی چگونه میتواند در یک موقعیت واقعی عمل کند. یک روند با پارامترهای \(k=0.25\) و \(b=10\) را در نظر بگیریم و کمی نویز به آن اضافه کنیم که به صورت انحرافات تصادفی توزیع شده است. با استفاده از نقاط بهدستآمده، سعی خواهیم کرد پارامترهای روند اولیه را پیدا کنیم. در نهایت، چیزی شبیه به این خواهیم داشت.
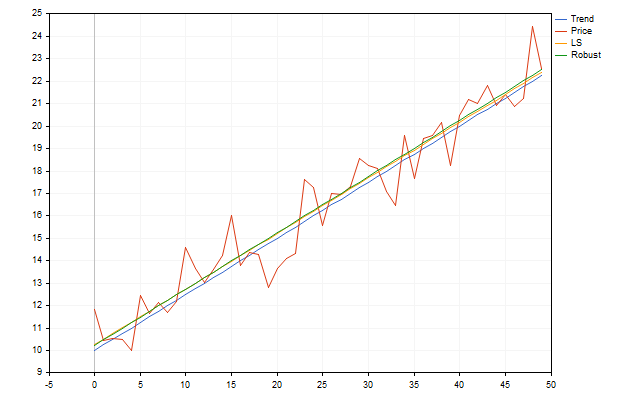
در نگاه اول، به نظر میرسد که این روش مقاوم (Theil-Sen) مزیت چندانی ندارد. اما این فقط به این دلیل است که خطاها در مدل روند ما به طور یکنواخت و بر اساس قانون نرمال توزیع شدهاند. قیمتهای واقعی ممکن است این معیار را برآورده نکنند. در این صورت، روش تیل-سن به مراتب بهتر عمل میکند و ممکن است اطلاعات بیشتری ارائه دهد. من از این تخمین مقاوم در آینده استفاده خواهم کرد.
حال بیایید نگاهی به چگونگی برآورد پارامترهای یک روند خطی با استفاده از روش تیل-سن بیندازیم. ابتدا باید پارامتر \(k\) را محاسبه کنیم. این پارامتر برابر با میانه تمامی تفاوتهای ممکن به شکل زیر خواهد بود:
![]()
مقدار میانه را میتوان به شکل زیر پیدا کرد. ابتدا تمام مقادیر را در یک آرایه بنویسید. سپس آن را مرتب کنید. میانه برابر با مقداری است که در مرکز آرایه قرار دارد.
اکنون میتوانیم به برآورد پارامتر \(b\) بپردازیم. برای این کار، باید میانه تمامی مقادیر ممکن را پیدا کنیم:
حالا که نظریه را بررسی کردیم، زمان آن رسیده که به عمل بپردازیم. بیایید ببینیم استفاده از تخمین تیل-سن چه امکاناتی برای ما فراهم میکند.
تخمین تیل-سن و شاخصها
پس از برآورد پارامترهای روند، دو آرایه داده در اختیار داریم. بیایید ببینیم آیا میتوانیم از این آرایهها به طریقه دیگری استفاده کنیم.
بنابراین، ما پارامترهای روند را ارزیابی کرده و حتی خط آن را ساختهایم. اکنون میتوانیم کانالی بسازیم که حرکت قیمت در آن انجام میشود. برای این کار، ابتدا باید ارزیابی کنیم که قیمتها چقدر از خط روند منحرف شدهاند.
بیایید از آرایهای که هنگام برآورد پارامتر \(b\) استفاده کردیم، استفاده کنیم. برای برآورد انحراف، باید انحراف مطلق میانه را پیدا کنیم. یعنی، ابتدا برای هر عنصر آرایه، مقدار مطلق تفاوت آن با پارامتر \(b\) را محاسبه میکنیم. سپس باید میانه مقادیر بهدستآمده را پیدا کنیم. این میانه تخمینی مقاوم از انحراف استاندارد را ارائه خواهد داد.
با دانستن انحراف استاندارد، میتوانیم یک کانال روند بسازیم. به عنوان مثال، اینگونه است که یک کانال به عرض ۶ انحراف استاندارد به نظر میرسد.
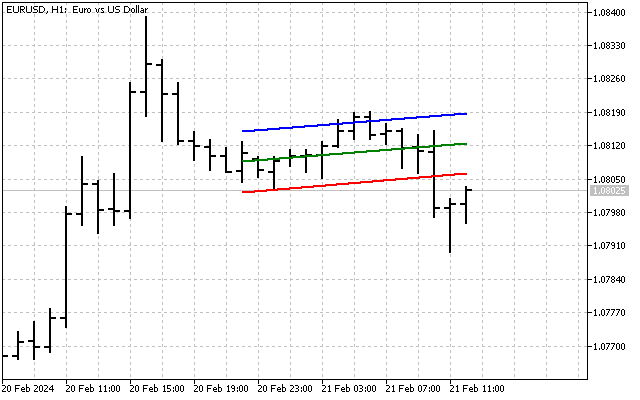
این شاخص اساساً مشابه باندهای بولینگر است. علاوه بر این، خطوط کانال روند میتوانند به عنوان سطوح حمایت و مقاومت استفاده شوند.
علاوه بر این، میتوانیم یک فن از خطوط روند بسازیم. تمام محاسبات به همان شیوهای انجام میشود که هنگام ساخت کانال انجام میدهیم. تنها تفاوت این است که باید پارامتر \(k\) و آرایه مربوطه را در نظر بگیریم. این تصویر یک فن است که با یک انحراف بهوسیله زاویه مشخص میشود.
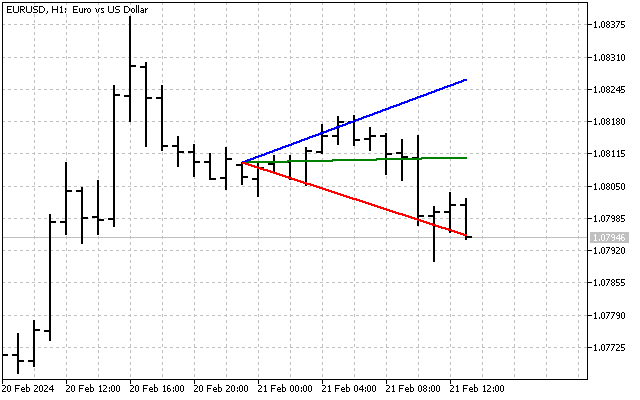
البته، میتوانیم کانال و فن را ترکیب کنیم. برای این کار، ابتدا خطوط کانال را رسم میکنیم. سپس فن را بر روی آنها اعمال میکنیم. در نتیجه، چیزی شبیه به این خواهیم داشت.
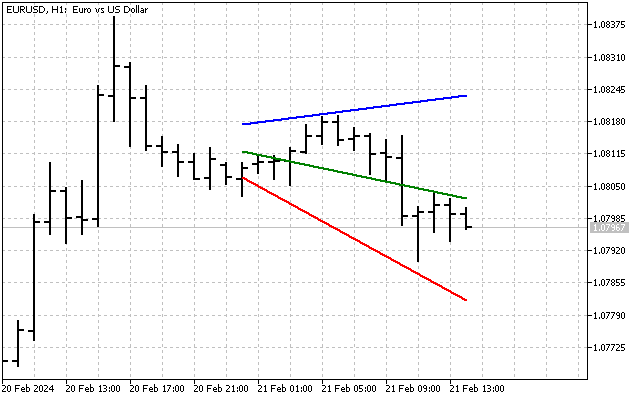
بنابراین، استفاده از روشهای مقاوم به ما این امکان را داد تا یک خط روند و سه شاخص اضافی بدست آوریم که میتوانند در تحلیل تکنیکال مورد استفاده قرار گیرند.
ملاحظات اضافی
عملیات مبتنی بر زاویه تنها برای ساخت روندها و زوایا قابل استفاده نیستند. بیایید به شاخص CCI که در مقاله قبلاً ذکر شد، اشاره کنیم. اگر ما شاخصی مشابه بسازیم و به جای قیمتها از زوایای روند استفاده کنیم، چه اتفاقی میافتد؟
در این صورت، میتوانیم تغییرات روند را بر اساس تاریخ مورد ارزیابی قرار دهیم. این چیزی است که شاخص ما به آن شکل خواهد بود.
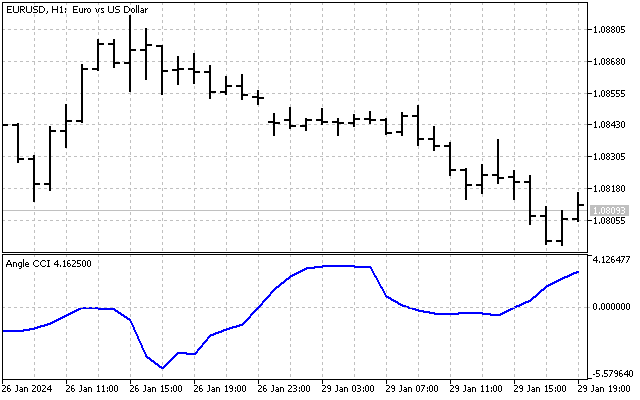
تمامی شاخصهای تکنیکال را میتوان به گونهای تنظیم کرد که با مقادیر زاویهای کار کنند. با این تغییرات، میتوانیم راههای جدیدی را در تحلیل تکنیکال کشف کنیم.
دانلود فایل های مربوط به مقاله
نتیجهگیری
برنامههای زیر در نوشتن این مقاله مورد استفاده قرار گرفتند.
| نام | نوع | توضیحات |
|---|---|---|
| Angle Two Pairs | شاخص | SecSymbol: نماد دوم برای تحلیل؛ iPeriod: دوره شاخص. |
| LS vs Robust | اسکریپت | مقایسه روش LSM و تخمین Theil-Sen. |
| Theil–Sen Estimator | شاخص | نوع: انتخاب نوع شاخص؛ iPeriod: دوره شاخص؛ StDevAngle و StDevB: تعداد انحراف معیار بر اساس زاویه و پارامتر b. |
| Angle CCI | شاخص | iPeriod: دوره شاخص. |










 معرفی کتاب «اسرار ترید حرفه ای» نوشته مهرداد داودی | راهنمای کسب درآمد از بازارهای مالی
معرفی کتاب «اسرار ترید حرفه ای» نوشته مهرداد داودی | راهنمای کسب درآمد از بازارهای مالی 















نظرات کاربران